Compressing Neural Networks: Towards Determining the Optimal Layer-wise Decomposition

Link: https://arxiv.org/pdf/2107.11442.pdf

저자/학회 특이사항

• Neurips 2021 Accepted Paper
• 저자는 MIT CSAIL과(Lottery paper 나오는 그곳, 같은 저자는 아님) Haifa 대학(이스라엘)으로 구성되어 있음.

Introduction

• 논문은 기본적으로 DNN을 압축하는 방법으로 Low-rank Approximation (LRA)을 제안함. 사실 LRA의 한계가 뚜렷하다고 생각하고, 최근에 재미있는 LRA 논문이 거의 없다시피 했는데, 오랜만에 만나는 LRA 논문이라 어떤 새로운 내용이 있을까 흥미롭게 보기 시작.
• SVD를 이용한 LRA는 기본적으로 2D matrix를 분해(decomposition)하고, rank를 줄여서 approximation되고 메모리와 연산량이 줄어들도록 2개의 decomposed layer를 만드는게 기본임.
• 여기서는 4D conv. tensor를 주로 사용하는 것으로 보이기 때문에 Tucker Decomposition[1]과 같은 방법을 쓰는지, 아니면 Lowering후에 Decomposition[2]을 하는지도 궁금하고, approximation으로 인한 degradation은 어떻게 극복하는지, fine-tuning인지, re-training인지 궁금했음.
• 다만, 제목에서도 볼수 있듯이 이 논문은 상당 부분의 초점은 Global하게 최적의 rank를 정하는 것에 초점이 있음. 즉, layer마다 압축율을 다르며, global한 Compression Ratio(CR)을 만족하는 범위내에서 최대한 layer별 각각의 rank를 구하는 것을 목표로 하는 것 같음.
• 최근, NAS를 이용한다던지 해서 layer 별로 loss에 미치는 sensitivity가 다르다는 것을 고려한 논문들이 여럿보인다. 또 비슷한 논문들을 학회 리뷰를 하면서 reject 시켰던 여러 경험이 있었는데, 이 논문은 뭐가 달라서 Neurips에 당첨되었는지 봐야할것 같다.

ALDS

• 제안하는 Compression Framework의 이름은 ALDS (Automatic Layer-wise Decomposition Selector)이다.
• 
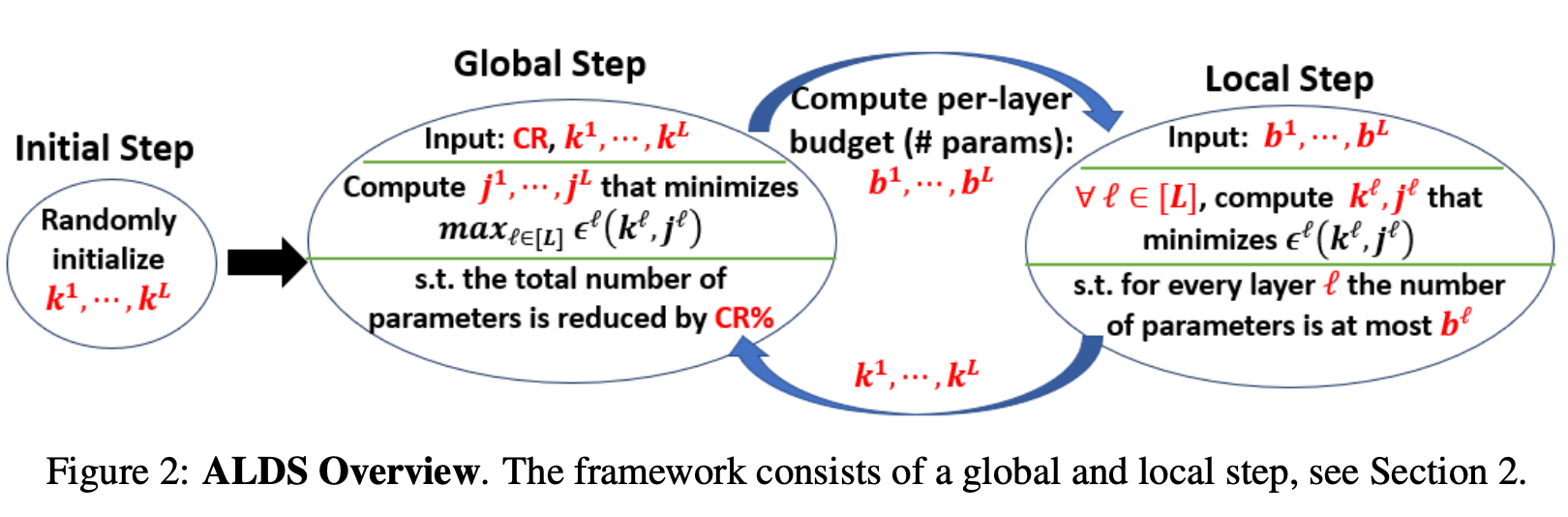
• 기본적으로 Global step과 Local step을 반복하는 것을 알 수 있다.
• Global Step은 CR(목표 압축율)과 k_{1…L}(각 layer별 decomposition subset의 개수)을 받아서, 각 layer마다 parameter number constraints(b^{1…L})을 Local Step에 전달한다.
• Local Step은 주어진 layer별 budget을 들고 그것을 만족시키는 k를 다시 구해서 Global Step으로 넘기고
• Iterative하게 반복하다가 error가 converge될때 종료한다.

SVD 하는 방법 (k가 대체 무엇이냐?)

• 기본적으로 4d tensor를 SVD하는 방법은 f filter, c channel, 3x3 conv로 이루어진 (f, c, 3, 3) weight을 f x c x 3 x 3으로 folding(lowering)한 후에 f x j와 j x c x 3 x 3으로 LRA+SVD하는 방식. 이것을 다시 conv로 변환하면 (f,j,1,1) 1x1 conv layer와 (j,c,3,3) 3x3 conv layer로 구성시킬수 있음.
• 여기서 k값이 다시 등장하는데, channel 방향으로 k개로의 subset으로 나눈다. 잘 몰랐었는데, 오래전 Denton[3]의 논문도 그렇고, SVD를 하기 전에 여러개의 subset으로 나는 것이 효과적인 방법으로 여겨져왔던듯 하다.
• 
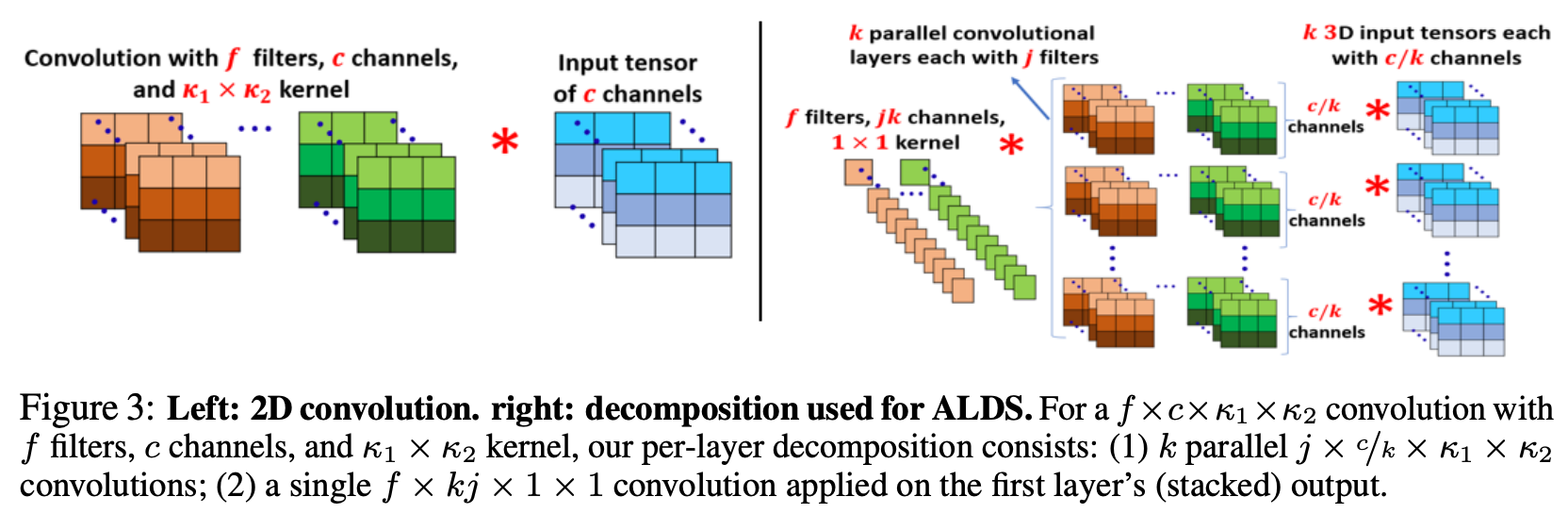
• 위 그림은 이 과정을 나타낸 논문의 Figure 3 그림이다. 왼쪽의 convolution layer + input 구성이 오른쪽처럼 Approximation 된다.
• 즉, 다음과 같은 과정이다. 1) input channle f에서 output channle c로 가는 conv를 f에서 jk로 reduction을 시키고, 2) channel을 k개로 나눠서 j개의 input channel을 c/k의 output channel로 보내는 (j, c/k, 3, 3) conv를 k개 돌리게 된다.
• 이 구조는 Group Conv.와 같은 구조이다. 결국 Layer Decomposition의 결과로 1x1 conv.와 group conv.로 이루어진 경량 conv.를 만든다고 무방할 것 같다.

Global Step에서 Layer별로 rank와 k (group conv의 개수)를 optimization 하는 방법

• 논문에서 여러차례 언급하고 있듯이, 모든 경우를 다 탐색해볼 수는 없다. 그래서 여기서는 minimizing the maximum relative error incurred across layers라는 방법을 사용한다.
• Relative error는 decompistion 전후의 weight 값의 차이의 norm을 original weight의 norm으로 나눈 값이다 (Equation 1). 이 값을 모든 layer가 비슷한 값을 가지도록 누른다는 뜻은, 모든 layer에 골고루 error가 들어가도록 함으로써 어떤 특정 layer를 망가뜨리지 않겠다는 뜻이다.
• 2.2장에서 복잡한 증명이 있는데, 2.3장의 알고리즘이 바운드 된다는 것은 증명하는 내용으로 보인다.
• 2.3장에서는 이것을 알고리즘으로 보여주고 있는데, 결국 heuristic하게, k값 정해보고 (처음에는 random), locally SVD 해보고, error를 기록하고, 이것을 converge할때까지 반복하는 것이다.

Retraining 방법

• Renda의 Rewinding paper[4]에서 영향을 받았다고 한다.
• e epoch 돌린 Pre-trained model이 만들고, compression을 하고, r epoch동안 [e-r, e] epoch에서 사용된 hyperparameter로 re-training을 한다. 그리고 이 과정을 계속 반복한다.

Results

• 
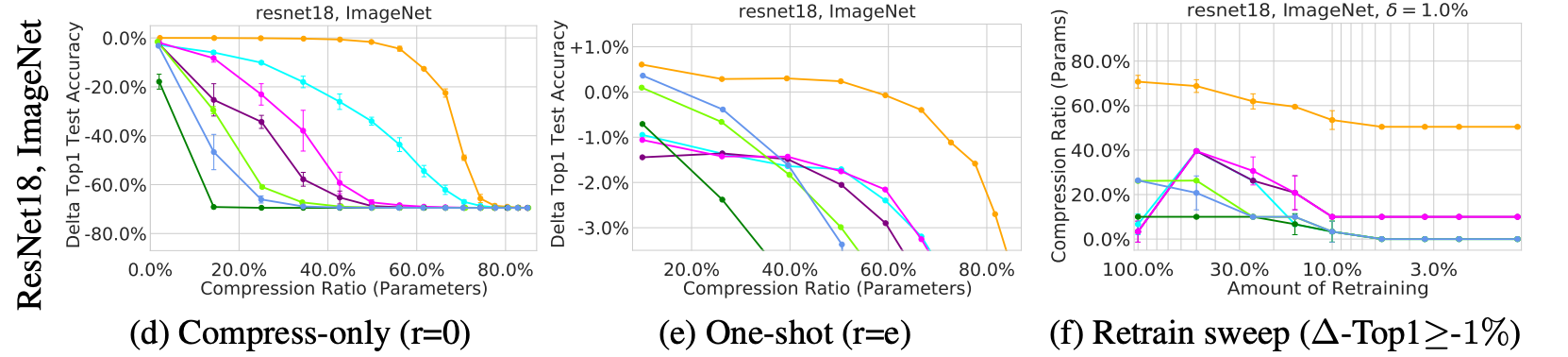
• 결과는 좋은 그림을 그리고 있다. 첨에는 왜 그럴까 싶었는데, 그냥 1x1과 group conv로 이루어진 새로운 arch.를 만들기 때문인것 같다.
• 때문에 기존의 SVD 방법들과 정성적인 비교는 불가능할 것 같다. 어찌보면 당연히 성능 개선이 있어야하는 상황으로 보여진다. 오히려 1x1, group conv.를 적극 쓰는 그 이후의 경량 네트워크들과 비교해야할 것 같다. 게다가 layer-wise로 다른 rank를 주기 때문에 기존의 SVD 방법론들과 1:1비교는 불가능할것 같다.
• 그러니까 ResNet까지 밖에 못했을 것이라는 추정이 가능하다. 다른 경량 CNN에는 적용할수가 없을것 같다.

총평

• minimizing the maximum relative error라는 방법은 한번 생각을 해볼 필요가 있을것 같다.
• 사실 경량 네트워크 관점에서 페이퍼를 다시 써야하는게 아닌가 싶다. Borderline에서 살짝 점수를 잘 받은듯. Appendix를 봐도 그렇고 정성이 묻어나오는 페이퍼이긴 하다.

[1] Kim, Y. D., Park, E., Yoo, S., Choi, T., Yang, L., & Shin, D. Compression of deep convolutional neural networks for fast and low power mobile applications. ICLR 2016.

[2] Lee, D., Kwon, S. J., Kim, B., & Wei, G. Y. Learning low-rank approximation for cnns. arXiv preprint arXiv:1905.10145.

[3] Denton, E. L., Zaremba, W., Bruna, J., LeCun, Y., & Fergus, R. Exploiting linear structure within convolutional networks for efficient evaluation. NIPS 2014.

[4] Renda, A., Frankle, J., & Carbin, M. Comparing rewinding and fine-tuning in neural network pruning. ICLR 202.